OPアンプによるアナログ回路(2)

OPアンプによるアナログ回路(2)
2022/12/25 ※サーバー移行しました: http://cf661650.cloudfree.jp/altmo_toolbox

[Prev] [Next] [Top] , Analog Design [Prev] [Next]

ちょっと回路理論: 等価電圧源の定理

前回レポートで扱った回路は全て「抵抗1個のシンプルな帰還パス」でした。ですが設計要求の抵抗値が実在するとは限らないため、設計値を実現するために抵抗回路網を形成すると帰還パスが複雑になります。

すると回路網に対してループ電流解析等を適用し、連立方程式又は行列式を解いて...となりますが、それほど複雑ではない回路網ならば等価電圧源の定理(*1)を使って簡単化した方が楽です。

等価電圧源の定理とは「回路の任意の2点間で開放端電圧$V_{f}$、開放端インピーダンス$Z_{o}$がわかれば、その回路を電源$V_{f}$、出力インピーダンス$Z_{o}$の回路に置き換えられる」というものです。

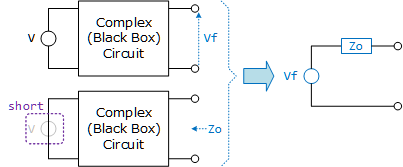
Figure 1: 等価電圧源の定理

使用例: 等価電圧源の定理

帰還パスの点線部に着目すると開放端電圧$V_{f}$は ${V_{o}}$を$R_{3}$と$R_{4}$で分圧した値、開放端インピーダンス$Z_{o}$は $V_{o}$をショートと見なすので、$R_{3}$と$R_{4}$の並列抵抗になります。

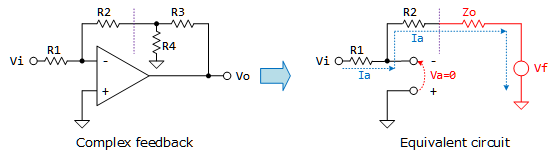
Figure 2: 等価電圧源の定理使用例 \[ V_{f}=V_{o}\frac{R_{4}}{R_{3}+R_{4}}, 　Z_{o}=R_{3}//R_{4}=\left(\frac{1}{R_{3}}+\frac{1}{R_{4}}\right)^{-1} \] \[I_{a}=\frac{V_{i}}{R_{1}}\] \[V_{a}-V_{f}=I_{a}(R_{2}+Z_{o})\] \[V_{f}=-\frac{V_{i}}{R_{1}}(R_{2}+(R_{3}//R_{4}))\] \[V_{o}\frac{R_{4}}{R_{3}+R_{4}}=-\frac{V_{i}}{R_{1}}(R_{2}+(R_{3}//R_{4}))\] \[V_{o}=-V_{i}\left(\frac{R_{2}+(R_{3}//R_{4})}{R_{1}}\right)\left(\frac{R_{3}+R_{4}}{R_{4}}\right)\]
最後に大事なことを。「等価電圧源の定理」は「重ね合わせの原理」から導かれます。この「重ね合わせの原理」が成立する前提条件は、対象が線形動作することです。

ローパスフィルタ

次は帰還パスにキャパシタが付いたOPアンプ回路です。抵抗とキャパシタを並列に入れるとローパスフィルタ(Low-pass filter)になります。

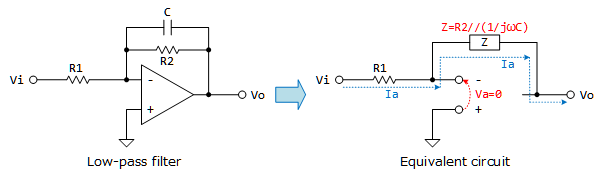
Figure 3: ローパスフィルタ

帰還パスのインピーダンスを $Z=R_{2}//C$ と表現してしまえば、$V_{i}$ と $V_{o}$ の関係は反転増幅回路と同じです。
\[Z=R_{2}//(1/j\omega C)=\left(\frac{1}{R_{2}}+j\omega C\right)^{-1}\] \[V_{o}=-V_{i}\frac{Z}{R_{1}}\]
周波数が高くなると$C$側のインピーダンスが低くなるため、帰還パスのインピーダンス$Z$も低くなります。結果として周波数が高い入力に対し出力$V_{o}$は$0$になります。一方周波数が低い場合は$R_{2}$が支配的となり、$-R_{2}/R_{1}$の増幅度で$V_{o}$が出力されます。

ハイパスフィルタ

次にハイパスフィルタですが、キャパシタを含むインピーダンス$Z$が、増幅の分母...入力側に付けば良いですね。つまりFigure 4の回路になります。

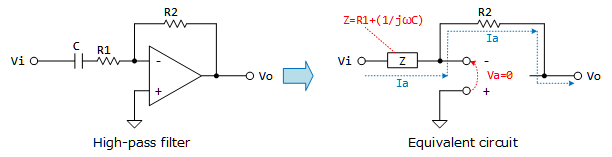
Figure 4: ハイパスフィルタ
\[Z=R_{1}+\frac{1}{j\omega C}\] \[V_{o}=-V_{i}\frac{R_{2}}{Z}\]
周波数が高い場合は$R_{1}$だけが残り、増幅度$-R_{2}/R_{1}$で出力されます。周波数が低い場合は$Z$が大きくなるため、増幅度/出力は$0$に近づきます。

これでまずは読めるように

線形動作するOPアンプ回路について紹介してきました(*3)。仮想短絡と等価電圧源の定理を使うことで、アナログ演算の回路はかなり読みやすくなります。あとは先人の設計した回路を読みながら「設計のコツ」をもらっていきましょう。

Notes

[Prev] [Next] [Top] , Analog Design [Prev] [Next]